datetime-add
Returns an xs:dateTime value obtained by adding a duration (the second argument) to a datetime (the first argument).
Languages
Built-in, C++, C#, Java.
Parameters
Name | Type | Description |
|---|---|---|
datetime | xs:dateTime | Provides the xs:dateTime value to be used as input. |
duration | xs:duration | Provides the xs:duration value.
An example duration is P1Y2M3DT04H05M59S, where:
•"P" is the period designator, and is mandatory; •The rest of the characters denote, in this order: 1 Year, 2 Months, 3 Days, T (Time designator), 04 Hours, 05 Minutes, 59 Seconds.
If the minus character appears before the "P" designator, this indicates a negative duration, for example: -P1D. |
Example
Let's assume that the input datetime value is 2001-12-17T09:30:02+05:00. If the duration is P10D (10 days), the function's result is 2001-12-27T09:30:02+05:00.
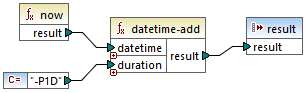
To obtain yesterday's date, connect the now function to the datetime input. In the mapping below, the period -P1D means "minus 1 day", so the mapping returns yesterday's date.